Week2 关于我摸鱼的第二次研究生组会

汇报内容

上周对论文《An Eﬀicient Coq Tactic for Deciding Kleene Algebras》进行解读，首先将Kleene Algebras使用符号进行解释，其次对Kleene Algebras的符号表示使用有限自动机理论进行解释，其中自动机理论转化为正则表达式进行解释。
1、决定Kleene Algebras中的等式
有限自动机理论：正则语言相等条件，当且仅当相应的最小自动机是同构的。
表达式a,b表示相同的正则语言，那么在任意Kleene Algebras中都能证明a=b。
Kleene Algebras中的A元素可以有三个矩阵表示<u,m,v>，其中u,v是0-1向量，M表示转化矩阵，u为初始态，v为接受态，Kleene Algebras上的方阵形成Kleene Algebras。

2、潜在的设计选择
定义代数层级、矩阵表示、异构结构处理、物化机制、数字表示。
代数层级Kleene Algebras{单类：monoid，半格：semi-lattice}。
矩阵：整数对->type X的部分映射。
类型化代数、类型具体化（类型具体化coq不处理类型结构，ltac中实现，具体化时间长于计算时间，在Ocaml中实现）。
数字、有限集、有限映射。

3、算法和证明
判断两个正则表达式相同的语言分为四步。1、e-NFA构造非确定有限自动机。2、移除e-transitions获得NFA。3、获得DFA。4、检查两个DFA等效图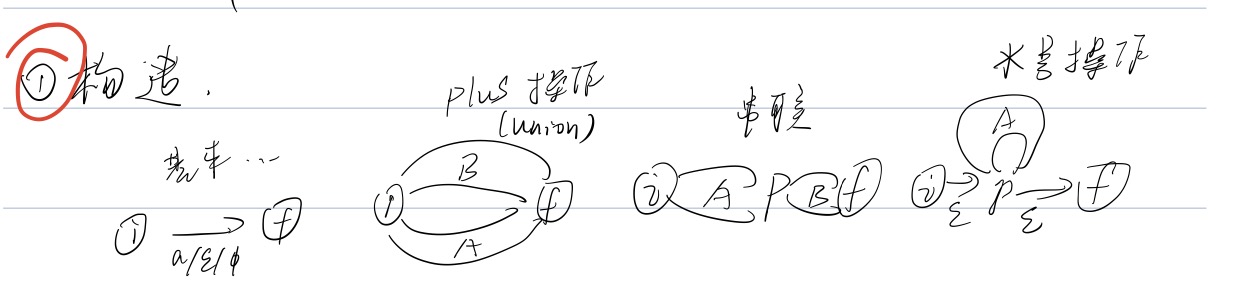

为避免union操作，使用累加器递归添加转台和转化。

e-transitions移除
1）递归函数，以严格的star形式将正则表达式转化为等价正则表达式
2）证明当参数是严格star形式，本文构造算法返回的e-NFAs的反转（reversed）的e-transitions是有依据的
3）基于上述假设，使用更具的递归和memoisationl实现线性传递闭包
4）证明算法产生了NFA.t自动机，且为<u·J*，N·J*，v>